Accurate expressions for optical coefficients, due to the impurity-size effect, and obtained in n(p)-type degenerate Si crystals, taking into account their correct asymptotic behavior, as the photon energy E (\rightarrow\infty)
DOI: 10.54647/physics140547 101 Downloads 13650 Views
Author(s)
Abstract
In our three previous papers [1, 2, 3], referred to as I, II and III. In I and II, our new expression for the static dielectric constant, \varepsilon\left(r_{d\left(a\right)}\right), r_{d\left(a\right)} being the donor (acceptor) d(a)-radius, was determined by using an effective Bohr model, suggesting that, for an increasing r_{d\left(a\right)}, \varepsilon\left(r_{d\left(a\right)}\right), due to such the impurity size effect, decreases, and affecting strongly the critical d(a)-density in the metal-insulator transition (MIT), N_{CDn(CDp)}(r_{d(a)}), determined by Eq. (3), and also the optical coefficients, given in the n(p)-type degenerate Si crystal, at low temperature T and high d(a)-density N, according to the reduced Fermi energy \xi_{n(p)}(\geqq1), since those coefficients are expressed in terms of \left(E^\ast\equiv E-\mathbb{E}_{gn(gp)}\right)^2. Here, E^\ast is the effective photon energy, E is the photon energy and \mathbb{E}_{gn(gp)} is the band gap, which can be equal to the intrinsic band gap \mathbb{E}_{gni(gpi)}({\ r}_{d(a)}), and optical band gap \mathbb{E}_{gn1(gp1)}({\ N^\ast,r}_{d(a)},T), as those defined in Eq. (5), noting that N^\ast is the effective d(a)-density, defined by: N^\ast\equivN-N_{CDn(CDp)}(r_{d(a)}), being the effective density of free electrons (holes), given in the parabolic conduction (valence) bands of the n(p)-type degenerate d(a)-Si crystals. Then, using the same physical model and same mathematical methods and taking into account the corrected values of energy-band-structure parameters, all the numerical results of the optical coefficients, obtained in III, are now revised and performed, giving rise to some important concluding remarks, as follows.(i)The physical MIT-condition for N, is found to be given by: N^\ast\equivN-N_{CDn(CDp)}(r_{d(a)})=0 or N=N_{CDn(CDp)}(r_{d(a)}), which can be explained by the density of electrons (holes) localized in the exponential conduction(valence)-band tails, N_{CDn\left(CDp\right)}^{EBT}({\ r}_{d(a)}), determined in Eq. (21), with a precision of the order of {10}^{-5}, as given in Table 1.(ii) By basing on correct asymptotic behaviors of the refraction index n and extinction coefficient \kappa, as those proposed in Equations (28, 29), we have investigated all the optical coefficients, being determined in Equations (24, 25, 28, 29), and then their numerical results given in different physical conditions have been tabulated and discussed in Tables 2a(b, c), 3a(b, c), 4n(p), 5n(p), and 6n(p), in which \mathbb{E}_{gni(gpi)} and \mathbb{E}_{gn1(gp1)}, defined in Eq. (5), play a very important role.(iii)As given in Eq. (30), at T=0K, the physical MIT-condition for E, is that \kappa(E^\ast=0,\ r_{d(a)})=0, at E^\ast\equivE-\ \mathbb{E}_{gni(gpi)}=0, according to the critical photon energy {E=E}_{CPE}=\ \mathbb{E}_{gni(gpi)}, being similar to the physical MIT-condition for N, as that given in (i). (iv) As showed in Tables 3a, 3b and 3c, our expressions for optical coefficients are found to be more accurate than the corresponding ones, being obtained from the physical model proposed by Forouhi and Bloomer [11]. (v) Finally, as showed in Tables 4n and 4p, the extrema values of real (imaginary) parts of the complex dielectric functions, \varepsilon_{1(2)}(E, r_{d(a)}), given in any d(a)-Si systems, occur at the same photon energy E.
Keywords
Effects of the impurity-size and heavy doping; effective autocorrelation function for potential fluctuations; optical coefficients; critical photon energy
Cite this paper
H. Van Cong,
Accurate expressions for optical coefficients, due to the impurity-size effect, and obtained in n(p)-type degenerate Si crystals, taking into account their correct asymptotic behavior, as the photon energy E (\rightarrow\infty)
, SCIREA Journal of Physics.
Volume 8, Issue 3, June 2023 | PP. 172-197.
10.54647/physics140547
References
| [ 1 ] | H. Van Cong,Same maximum figure of merit ZT(=1), due to effects of impurity size and heavy doping, obtained in the n(p)-type degenerate Si-crystal 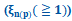 at same reduced Fermi energy at same reduced Fermi energy 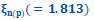 and same minimum (maximum) Seebeck coefficient and same minimum (maximum) Seebeck coefficient  , at which same , at which same 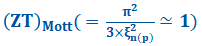 , SCIREA J. Phys., vol.8, pp. 66-90 (2023). , SCIREA J. Phys., vol.8, pp. 66-90 (2023). |
| [ 2 ] | H. Van Cong, “New dielectric constant, due to the impurity size effect, and determined by an effective Bohr model, affecting strongly the Mott criterion in the metal-insulator transition and the optical band gap in degenerate (Si, GaAs, InP)-semiconductors, “SCIREA J. Phys., vol.7, pp. 221-234 (2022); H. Van Cong et al., “Size effect on different impurity levels in semiconductors,” Solid State Communications, vol. 49, pp. 697-699(1984). |
| [ 3 ] | H. Van Cong, “Effects of donor size and heavy doping on optical, electrical and thermoelectric properties of various degenerate donor-silicon systems at low temperatures,” American Journal of Modern Physics, vol. 7, pp. 136-165 (2018). |
| [ 4 ] | H. Van Cong et al., “A simple accurate expression of the reduced Fermi energy for any reduced carrier density. J. Appl. Phys., vol. 73, pp. 1545-15463, 1993; H. Van Cong and B. Doan Khanh, “Simple accurate general expression of the Fermi-Dirac integral and for j> -1,” Solid-State Electron., vol. 35, pp. 949-951(1992); H. Van Cong, “New series representation of Fermi-Dirac integral for arbitrary j> -1, and its effect on for integer j,” Solid-State Electron., vol. 34, pp. 489-492 (1991). |
| [ 5 ] | C. Kittel, “Introduction to Solid State Physics, pp. 84-100. Wiley, New York (1976). |
| [ 6 ] | M. A. Green, “Intrinsic concentration, effective density of states, and effective mass in silicon,” J. Appl. Phys., vol. 67, 2944-2954 (1990). |
| [ 7 ] | H. Van Cong et al., “Optical bandgap in various impurity-Si systems from the metal-insulator transition study,” Physica B, vol. 436, pp. 130-139, 2014; H. Stupp et al., Phys. Rev. Lett., vol. 71, p. 2634 (1993); P. Dai et al., Phys. Rev. B, vol. 45, p. 3984 (1992). |
| [ 8 ] | J. Wagner and J. A. del Alamo, J. Appl. Phys., vol. 63, 425-429 (1988). |
| [ 9 ] | D. E. Aspnes, A. A. Studna, “Dielectric functions and optical parameters of Si, Se, GaP, GaAs, GaSb, InP, InAs, and InSb from 1.5 to 6.0 eV”, Phys. Rev. B, vol. 27, 985-1009 (1983). |
| [ 10 ] | L. Ding, et al., “Optical properties of silicon nanocrystals embedded in a matrix”, Phys. Rev. B, vol. 72, 125419 (2005). |
| [ 11 ] | A. R. Forouhi, I. Bloomer, “Optical properties of crystalline semiconductors and dielectrics”, Phys. Rev., vol. 38, 1865-1874 (1988). |
| [ 12 ] | G. E. Jr. Jellison, F. A. Modine, “Parameterization of the optical functions of amorphous materials in the inter-band region”, Appl. Phys. Lett., vol. 69, 371-373 (1996). |

